Map navigation can be one of the greatest hurdles that new coders have to overcome. I like to think of your first navigation program as your trial before you start to uncover more difficult applications of coding. Before I wrote my first navigation program I would have considered myself to be a novice developer; however, once I had completed my first project I feel that I discovered thought processes and applications I had never had before. The learning possibilities that are presented from solving a truly difficult problem can be the cornerstone of your development and advancement. One of the most crucial parts of this learning opportunity is the denial to use outside code. You can refer to writing and tutorials, but do your best to write all of your code yourself.
So, how do you start navigating a map? The first step is understanding different methods of navigation. There are many complex algorithms in map navigation to solve mazes as fast as possible or find the shortest possible route between two points. However, most of these algorithms take advantage of one of two most basic navigation techniques: Breadth-first search and depth-first search.
Breadth-First Search (BFS) is the first algorithm that I attempted to implement and I feel that it is the easier of the two to code. The basic principle of BFS is that you search every possible step in tandem instead of choosing one path and dedicating to it before backtracking and checking another possible path. BFS is better at finding the shortest path in most instances since it checks all possible paths at once. However, it is harder to discern a path from a BFS’s result since most of your information will not be correlated to previous moves. I prefer to use BFS when a problem asks for the least possible moves to get from point A->B.
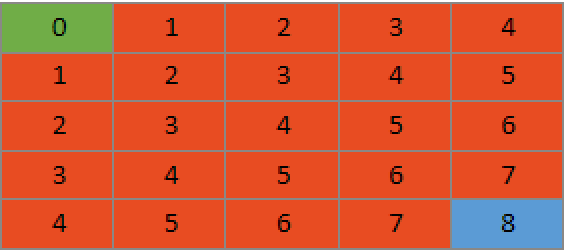
Depth-First Search (DFS) can be more difficult to implement since it is reliant on a greater understanding of recursion and structures such as queues or stacks. The basic principle of DFS is to take a point and choose a random direction repeatedly working around the map until you reach the endpoint. You search points and their possible paths discerning if they are a possible solution. If you reach a dead-end in your navigation you then backtrack until you create a path that is able to solve the map. The greatest downside with DFS is that is not guaranteed to find the shortest navigation of the map. This is best used in tandem with BFS to find the length of the shortest possible path and then find out which path is able to solve the map while using the number of moves specified by the BFS search. You would want to use a DFS when you want an exact path through a maze.
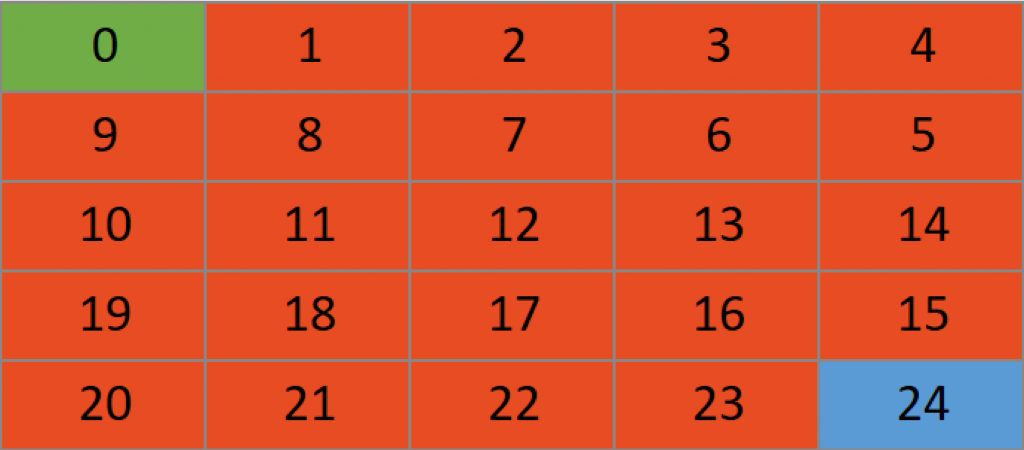
The most basic element of map navigation is to understand the algorithm that you want to create in your code. Now that you understand the most basic search procedures in a map the next step in navigating a map would be to transition the thought approach of navigation into code. This can be tedious and will be hard in the beginning, but you must push through to advance your knowledge through the process.